
C#에서는 이미지를 2차원 배열로 다루게 됩니다.
이번 포스팅은 C#에서 2차원 배열을 순회하는 여러 가지 방법에 대해 알아보고
작업 속도를 비교해 보겠습니다.
| 왜 이미지를 2차원 배열로 사용하는가?
C#에서는 이미지를 2차원 배열로 다루게 됩니다.
그 이유는 이미지 데이터의 특성 자체를 이해하기 위해서입니다.
이미지는 픽셀로 구성되어 있으며, 각 픽셀은 화면에서 특정 위치를 나타냅니다.
이 위치는 바로 이미지의 x 좌표와 y 좌표, 즉 2차원의 공간으로 표현됩니다.
이미지를 2차원 배열로 표현하면, 배열의 각요소가 이미지의 픽셀 하나를 나타내게 되며
배열의 인덱스가 바로 픽셀의 위치 (x, y)를 나타내며 인덱스에 저장된 값은 해당 픽셀의 색상 정보를 나타냅니다.
따라서 이미지를 2차원 배열로 다루면 각 픽셀의 위치와 색상 정보에 대해 쉽게 접근하고 조작할 수 있습니다.
그러나, 실제로 이미지를 처리할 때는 각 픽셀이 R, G, B 세 가지 색상 채널을 가지고 있기 때문에,
실제로 3차원 배열을 사용하는 경우가 많습니다.
이 경우 배열의 첫 번째 차원은 이미지의 높이, 두 번째 차원은 넓이, 세 번째 차원은 색상 채널을 나타냅니다.
하지만 그레이스케일 이미지는 2차원 배열로 충분히 표현될 수 있으며
실제로 우리가 만드는 프로젝트에 따라 달라질 수 있습니다.
| 이중 For문을 사용한 2차원 배열 순회
C#에서 2차원 배열을 순회하는 가장 간단한 방법은 두 개의 중첩된 for 루프를 사용하는 것입니다.
예시) 중첩 for문을 사용한 2차원 배열 순회
int[,] array = new int[4096, 28000];
for (int i = 0; i < array2D.GetLength(0); i++)
{
for (int j = 0; j < array2D.GetLength(1); j++)
{
// 배열 요소에 1을 더하는 작업
array[i, j]++;
}
}
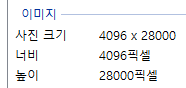
위에 보여드린 이미지의 픽셀 (4096, 28000)을 예시로 배열을 만들고
중첩 for문을 이용하여 배열을 순회하면서 배열 요소에 1을 더하는 코드입니다.
GetLength(0)은 배열의 첫 번째 차원(행)의 길이를 반환하고
GetLength(1)은 두 번째 차원(열)의 길이를 반환합니다.
4096 x 28000 같이 큰 규모의 데이터를 처리할 때는 이중 for문을 사용하면 처리 속도가 느립니다.
| 병렬 처리를 사용한 2차원 배열 순회
.Net 4.0 이상부터 Parallel.For을 사용한 병렬 처리를 수행할 수 있습니다.
이는 여러 코어를 활용하여 루프의 반복을 동시에 수행하므로, 큰 규모의 데이터를 빠르게 처리할 수 있습니다.
int[,] array2D = new int[4096, 28000];
Parallel.For(0, array2D.GetLength(0), i =>
{
for (int j = 0; j < array2D.GetLength(1); j++)
{
// 배열 요소에 1을 더하는 작업
array[i, j]++;
}
});
| 두 가지 방법에 대한 처리 속도 확인 결과

C#의 Stopwatch 클래스를 이용하여 처리 속도를 확인해 봤습니다.
약 2.5배 ~ 3배의 처리속도 차이를 보여줬습니다.
| 마무리
2차원 배열을 순회하는 방법 두 가지에 대해 알아보았습니다.
이러한 방법도 충분하지 않다면, 더 고급진 병렬 처리 기법이나 데이터 분할 기법을 고려해야 합니다.
다음 포스팅은 데이터 분할 기법을 사용한 2차원 순회 방법에 대해 알아보겠습니다.
질문이나 틀린 점이 있으면 댓글로 남겨주세요!
감사합니다 :)
'C#' 카테고리의 다른 글
| C# "System.InvalidOperationException: collection was modified enumeration operation may not execute." 에러 처리 방법 (0) | 2024.01.23 |
|---|---|
| C# 이미지의 2차원 배열을 순회하는 여러가지 방법 - 2 (2) | 2024.01.21 |
| C# Partial Class 이해 (0) | 2023.12.27 |
| C# 비동기 프로그래밍 : Event-based Asynchronous Pattern(EAP) 이해 (0) | 2023.11.27 |
| C# 비동기 프로그래밍 : deadlock 문제와 해결 방법 (0) | 2023.11.23 |
