변이형 오토인코더(Variational AutoEncoder) 이해 및 구현
GOAL
- 생성 모델링 중 오토인코더가 무엇인지 알고 작동 방법을 알아본다.
- 변이형 오토인코더를 MNIST 데이터 셋으로 간단하게 구현시켜 확인
오토인코더(AutoEncoder)란?
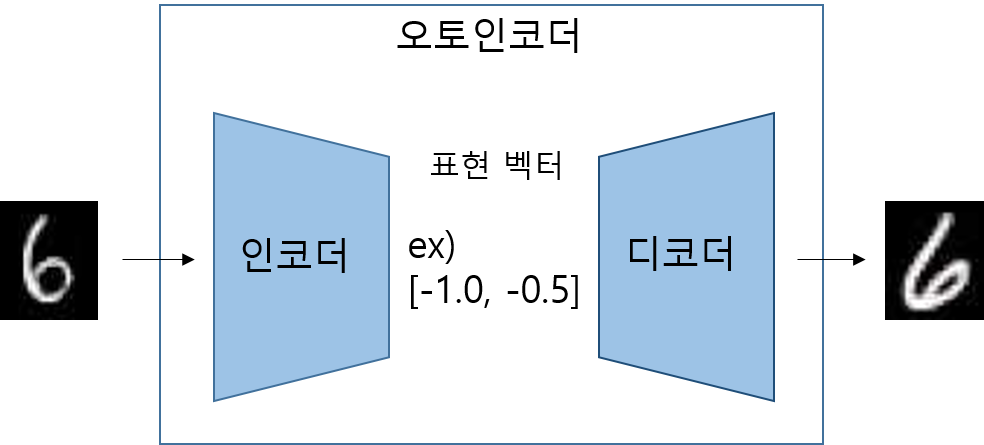
- 오토인코더는 인코더와 디코더로 이루어진 신경망
- 인코더(encoder) 네트워크 : 고차원 입력 데이터 -> 저 차원 표현 벡터(representation vector)로 압축
- 디코더(decoder) 네트워크 : 주어진 표현 벡터 -> 원본 차원으로 압축 해제
- 위의 그림은 오토인코더의 예시를 만들어 보았습니다. 원본 입력은 인코더와 디코더를 지나서 재구성된 이미지로 출력되며 네트워크는 입력과 재구성된 이미지 사이의 손실을 최소화하는 가중치 매개변수를 찾기 위해 훈련합니다.
- 표현 벡터라는 것은 원본 이미지를 저 차원 잠재 공간(latent space)으로 압축한 것을 2차원 벡터로 표시(예시)
실제로는 2개 이상의 차원을 가지며 이것은 이미지의 차이를 잘 감지하기 위해서입니다.
변이형 오토인코더(Variational AutoEncoder) 이해
- 오토인코더와 차이
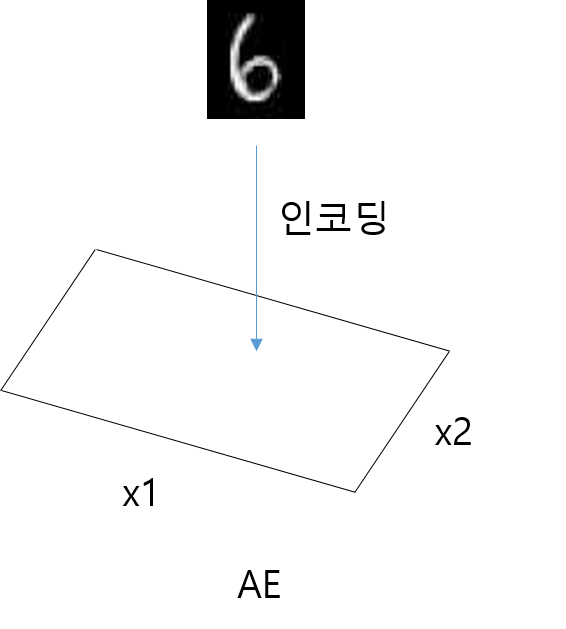
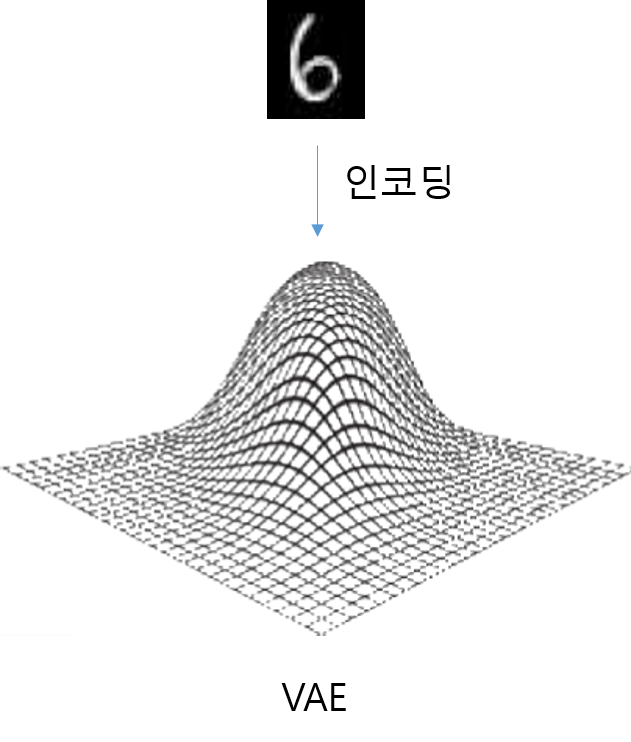
- AE는 입력 이미지가 잠재 공간(latent space)의 한 포인트에 매핑되는 형식이라면 VAE는 이미지가 latent space에 있는 포인트 주변의 정규 분포에 매핑됩니다.
- VAE는 latent space와 dimension 사이에 어떤 상관관계가 없다고 가정합니다. 이 뜻은 인코더가 각 입력 이미지를
평균 벡터와 분산 벡터에만 매핑할 필요가 있다는 뜻입니다.
- 코드를 보시면 분산에 log를 취해서 진행하는 것을 볼 수 있는데 이는 신경망의 일반적인 출력은 ( -무한대, +무한대 ) 범위의 모든 실수이지만 분산은 항상 양수이기 때문에 분산에 log를 취한 값에 매핑을 하게 됩니다.
- 이미지를 latent space의 특정 포인트 z로 인코딩하기 위해서 sampling 함수를 정의합니다.
def sampling(args : tuple):
z_mean, z_log_var = args
# epsilon : 표준 정규 분포에서 샘플링된 값
epsilon = K.random_normal(shape = (K.shape(z_mean)[0], latent_dim),
mean = 0., stddev = epsilon_std)
return z_mean + K.exp(z_log_var / 2) * epsilon- z_mean는 분포의 평균 벡터입니다.
- epsilon은 z_mean에서 얼마나 떨어져 표시해야 하는지 나타내는 것입니다.
- AE에서는 latent space를 연속적으로 만들 필요가 없었습니다. 한 점 포인트에 매핑했을 때 (-1.0 1.0)가 4를 표시하더라도 (-1.1 1.1)이 비슷할 필요가 없었습니다.
하지만 VAE에서는 z_mean 주변의 랜덤 한 지역에서 랜덤한 포인트를 생성하기 때문에 비슷한 이미지로 디코딩해야 합니다. 이는 디코더에서 본 적 없는 포인트를 매핑하더라도 그럴듯한 이미지가 생성될 수 있는 좋은 성질입니다.
손실 함수
- 이전 AE의 손실 함수는 원본 이미지와 재구성된 이미지 사이의 손실로만 구성되었습니다. 이를 reconstruction loss라 하며 VAE에서는 여기에 추가적으로 Kullback-Leibler divergence (KL 발산)을 사용합니다. >latent loss라고도 합니다.
- KL 발산은 확률 분포가 다른 분포와 얼마나 다른지를 측정하는 도구입니다. 여기에서는 평균이 k_mean이고 분산이 z_log_var인 정규 분포가 표준 정규 분포와 얼마나 다른지 측정해야 합니다. 이럴 경우 코드로 다음과 같이 계산합니다.
# 손실 함수 정의
kl_loss = -0.5 * K.sum(
1 + z_log_var - K.exp(z_log_var) - K.square(z_mean),
axis = - 1
)
- 여기에서 KL 발산이 뜻하는 것은 샘플을 표준 정규 분포( z_mean = 0, z_log_var = 0 )에서 벗어난 z_mean, z_log_var 변수로 인코딩하는 네트워크에 벌칙을 가하는 것입니다.
- 왜 VAE는 손실 함수에 kl_loss를 추가할까요? 어떤 도움이 있을까요?
1. latent space에서 포인트를 선택할 때 사용할 수 있는 잘 정의된 분포(표준 정규 분포)를 가지게 된다.
그렇게 되면 샘플링 시 이미지 분포에 가까운 영역 안의 포인트를 선택할 가능성이 높아집니다.
2. kl_loss가 모든 인코딩 된 분포를 표준 정규 분포와 가깝게 되도록 합니다.
이는 포인트 사이의 간격이 커질 가능성을 낮게 해 줍니다.
변이형 오토인코더(Variational AutoEncoder) 구현 및 결과
- 인코더
# 함수형 API
# 인코더
x = Input(shape=(original_dim,), name = "input") # 인코더 입력
h = Dense(intermediate_dim, activation='relu', name = 'encoding')(x) # 중간층
z_mean = Dense(latent_dim, name="mean")(h) # 잠재 공간의 평균
z_log_var = Dense(latent_dim, name="log-variance")(h) # 잠재 공간의 분산
z = Lambda(sampling, output_shape = (latent_dim,))([z_mean, z_log_var])
encoder = Model(x, [z_mean, z_log_var, z], name="encoder") # 인코더를 정의
- 디코더
# 디코더 만들기
input_decoder = Input(shape=(latent_dim,), name="decoder_input") #입력
# latent space를 중간층의 차원으로 변환
decoder_h = Dense(intermediate_dim, activation='relu', name = "decoder_h")(input_decoder)
# 원본 차원으로 변환
x_decoded = Dense(original_dim, activation = 'sigmoid', name = "flat_decoded")(decoder_h)
decoder = Model(input_decoder, x_decoded, name = "decoder")
- 결합
# 모델 결합 - VAE 만들기
# 인코더의 출력을 디코더에 사용, 인코더의 세번째 변환 값이 z다.
output_combined = decoder(encoder(x)[2])
vae = Model(x, output_combined)
vae.summary()결과
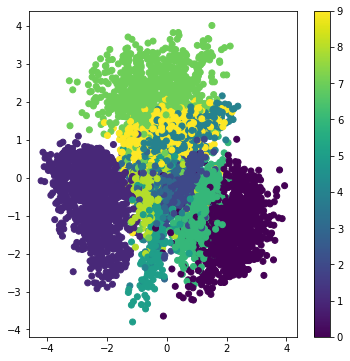

- 결과를 보시면 비슷한 숫자의 포인트끼리 군집해 있는 것을 볼 수 있고
실제로 포인트들을 꺼내어 확인해보면 있을 법한 손글씨 숫자들을 생성한 것을 볼 수 있습니다.
- AE에서 인코더와 손실 함수의 수정만으로 생성 모델로서 향상된 성능을 내는 것을 확인했습니다.
- 생성 모델 중 AE를 간단하게 알아보고 VAE에 대해 알아보았습니다. 생각보다 제법 있을 법한 이미지들을 뽑아내는 것을 보고 성능이 나쁘지 않다고 생각되었고 관심이 더 생기게 되었습니다.
- 질문이나 틀린 점이 있으면 댓글로 남겨주세요!
감사합니다 :)